Cristal Polarizador: Breve historia de las matemáticas III: Antigua Grecia (I)

El término matemáticas griegas comprende a las matemáticas desarrolladas en Grecia en el periodo comprendido entre 600 a. C. hasta el 300 d. C.

Lo primero que le debemos a los griegos es el nombre mismo de las matemáticas, que viene de la palabra mathemas, significa "campo de estudio" y se refiere a las áreas del conocimiento que sólo se pueden entenderse tras haber sido instruido en las mismas, en contraposición de musiké que se reafiere a la poésica, a la retórica y similares. Más tarde se le llamarían Mathematikos a quienes estudiaban los cuatro campos del saber según Pitágoras y Platón: aritmética, música, astronomía y geometría.

Los historiadores ponen el comienzo de las matemáticas griegas en la era de Tales de Mileto, primer hombre al que se la atribuye un teorema: el famoso Teorema de Tales, hoy en día conocido como Teorema de Tales - Les Luthiers ;-)

De este teorema se deduce la propiedad ilustrada en la siguiente imagen:

Imagen, modificada, de la wikipedia.

Según Herédoto, y tal como nos cuentan en la escuela, Tales utilizó esta propiedad para medir la altura de la pirámide de Keops.

El segundo teorema de Tales no es tan popular como el primero: Sea C un punto de la circunferencia de diámetro [AB], distinto de A y de B, entonces el ángulo $A\^{B}C$ es recto.

Imagen de la Wikipedia.

Pero más importante que lo que estos teoremas afirman, y que es el gran legado de los griegos, es el proceso deductivo basado en la lógica, axiomas y definiciones. Esto dista mucho de los babilonios y, sobre todo, de los egipcios, cuyas matemáticas eran más bien "empíricas", es decir, basadas en la observación. De hecho, parece ser que muchos de los descubrimientos atribuidos a los primeros matemáticos griegos ya era conocido por las egipcios y babilonios, y que probablemente los aprendieron de ellos. Sin embargo, fueron los griegos quienes hicieron las demostraciones. Ellos ya no veían los rectángulos como parcelas de tierra o los cilindros como vasijas, sino que hablaban de rectángulos y cilindros: desarrollaron la abstracción matemática.

Pero sigamos. Un matemático que no necesita presentación es Pitágoras. Su famoso teorema, $A^2 + B^2 = C^2$, el que probablemente sea el primer teorema que has aprendido, tiene cientos de demostraciones conocidas. En su libro, The Pythagorean Proposition, E. S. Loomis catalogó 367 pruebas diferentes. Aquí hay una fácil y rápida:

Otra de las grandes demostraciones de los pitagóricos es la de que $\sqrt{2}$ no puede escribirse como fracción. Una versión moderna de esa prueba es la primera demostración que uno aprende en la carrera (al menos en Argentina); yo la conocí antes leyendo el apéndice de Cosmos. Y no me puedo resistir a ponerla aquí, para que sea también la primera demostración en mi blog. Puedes saltearla si te atemoriza >: ]

*****

Si trazamos una diagonal en una cuadrado de lado uno, entonces, por pitágoras, sabemos que esta mide:

$C^2=A^2+B^2 = 1^2 + 1^2 = 2$

Por lo tanto:

$C^2=2$

$C=\sqrt{2}$

Si $\sqrt{2}$ se puede escribir como cociente de enteros, entonces existen $p$ y $q$, enteros y primos entre sí (no tienen factores comunes), tales que

$\sqrt{2}=\frac{p}{q}$.

Pero entonces:

$\sqrt{2} q = p$

$2 q^2 = p^2$

Luego, $p^2$ es un número par, pero el cuadrado de un número es par sólo si ese número es par. Por lo tanto $p$ es par y se puede escribir como $p = 2s$. Entonces

$p = 2s = \sqrt{2} q$

$p^2 = 4s^2 = 2 q^2$

Y dividiendo lo anterior por dos:

$2s^2 = q^2$

O sea que $q^2$ es par, por lo que $q$ es par. Pero si tanto $p$ como $q$ son pares, ambos son divisibles por dos, lo que significa que este es un factor común, y esto contradice uno de nuestros supuestos. Llegamos a un absurdo. Como el argumento no puede decirnos que esté prohibido reducir los factores comunes, que 1/2 esté permitido pero no 2/4, entonces el error está en suponer que $p$ y $q$ eran enteros. Luego $\sqrt{2}$ no puede escribirse como cociente de números enteros.

(¿Ven por qué un matemático no tiene porqué ser bueno haciendo cuentas? En esta demostración no hicimos casi ninguna)

*****

Este resultado fue doloroso para los pitagóricos, ya que su filosofía ponía a los números como la base de toda armonía y orden en el universo. Como ellos creían que todo número se podía expresar como fracción, concluyeron que $\sqrt{2}$ no lo era: ¡había proporciones que no se podían expresar en números! Pobres pitagóricos. Tuvieron que esperar casi un siglo para que se desarrollada una nueva teoría de la proporción. Esta vino de la mano de Eudoxo y puede leerse en los Elementos de Euclides.

Los Elementos de Euclides son la primera obra fundamental de matemáticas que nos ha llegado, y aún hoy sigue siendo una obra maestra: su contenido no fue modificado hasta el siglo XIX. No sólo habla de geometría, tal como se cree, sino que trata de tanto geometría plana y espacial como de aritmética y álgebra. Se trata un compendio de las matemáticas elementales de la época ¡Y todas las demostraciones parten sólo de cinco axiomas!

Dos décadas después de la muerte de Euclides nace Arquímedes, una de los más grandes matemáticos y científicos de todos los tiempos. En matemáticas, usó método de exhausción para calcular la longitud de una circunferencia y obtener $\pi$. Esto lo hizo inscribiendo polígonos regulares en una circunferencia de radio unitario y circunscribiendo polígonos a la circunferencia. Así, a medida que se aumenta la cantidad de lados de los polígonos, estos se aproximan más y más a la circunferencia. (De haber utilizado un sólo los polígonos interiores o sólo los exteriores, podía haber caído en un análogo de la Paradoja de la escalera).

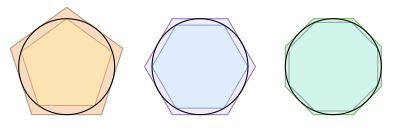Método de exhausción para hallar el área del círculo, la longitud de lacircunferencia y, como consecuencia, a $\pi$. Imagen de la Wikipedia.

Con este método hizo muchas otras demostraciones, incluyendo el primer cálculo de algunas series geométricas. También es famoso por estudiar la espiral que lleva su nombre, la cual hoy, en coordanadas polares, se expresa como $r=a+b\theta; a, b \in \mathbb{R}$

Espiral de Arquímedes. Imagen de la Wikipedia.

Aunque no es sea sencillo de ver, Arquímedes se adelantó muchos siglos a sus contemporaños estudiando esta espiral. Dado que esta no puede construirse utilizando sólo el compás y la regla, los griegos no le dieron importancia, salvo el mismo Arquímedes, que la utilizó para partir un ángulo en tres partes iguales. Esto último puede no parecer muy sorprendente, pero es que tampoco se puede partir un ángulo en tres partes iguales usando sólo el compás y la regla. Sin embargo, con el compás, la regla y la espiral, sí se puede.

Las varias obras de Arquímedes son perfectamente euclideas, es decir, siempre se parte de axiomas evidentes para llegar lógicamente a una conclusión.

Contemporáneo de Arquímedes, y otro de los grandes, fue Apolonio de Perga. A él le debemos el estudio más completo de las cónicas: circunferencia, elipse, hipérbola y parábola. Lamentablemente, se ha perdido casi todo su obra, salvo aquellas que Pappus menciona en su Tesoro del Análisis. Las cónicas, su obra más importante, nos ha llegado casi por completo: ocho de siete libros.

Todavía que hay más: Hisparco, Nicómaco, Herón, Ptolomeo y Diofanto y Pappus. Pero seguiremos en una segunda parte, que cada día los post me quedan más largos.

Breve historia de las matemáticas:

Links de interés: